ベクトル 内積の計算例

ベクトル　内積の計算例

内積の定義式は

そして、この定義から

また、内積では次のことが成り立つ

問題１　ベクトルの内積について、次のことを証明せよ。

【解】

（１）　内積の演算規則に従って計算するならば、次のようになる。

（２）　と考えて

馬鹿正直に計算してもいいけれど、（１）の結果を使うと

（３）

（証明終わり）

どの規則がどこで使われているかわかるように書いたけれど、実際計算するときには、このように計算する必要はない。

実数の展開の公式

などをつかって、実数の掛け算と同じようにベクトルの内積を計算すればよい。

次に、（２）の計算の幾何学的な意味を考えることにする。

△OABがあり、とすると、

となる。

そして、余弦定理から

つまり、問題１の（２）は余弦定理と同じものと考えることができ、ベクトルの簡単な計算で余弦定理を導いていることになる。

問題２　ベクトルについて、次の等式を証明せよ。

△ABCの辺BCの中点をMとし、

とするとき、上式からどのような定理が得られるか。

【解】

問題１の（１）、（２）より

上式の辺々を足し合わせると、

た

よって、

これは中線定理である。

（解答終わり）

問題１の（１）、（２）の結果を使わずに、

と、実際に計算しても苦労ではないけれど・・・。

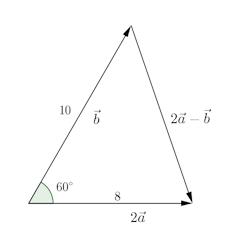
問題３　ベクトルの大きさがそれぞれ4、10で、のなす角が60°であるとき、の大きさを求めよ。

【解】

【別解】

余弦定理より