第１７回 陰関数定理

第１７回　陰関数定理

定義　（陰関数）

xとyに関する関係式f(x,y)=0に対して、関数y=φ(x)が

を満たすとき、y=φ(x)をf(x,y)=0によって定まる陰関数という。

例えば、f(x,y)=x²–y²–1= 0 とする。このとき、

とすれば、

となるので、とは関係式f(x,y)=x²–y²–1= 0 で定まる陰関数である。

定理　（陰関数定理）

点(x₀,y₀)を含む領域でf(x,y)はC¹級とする。

ならば、点(x₀,y₀)を含む近傍でf(x,y)=0の定めるC¹級の陰関数y=φ(x)がただ１つ定まり、次の関係が成り立つ。

【証明】

とする。

関数f(x,y)はC¹級だから点(x₀,y₀)のある近傍でである。

x=x₀で固定すると、だからf(x₀,y)はyに関して単調増加。

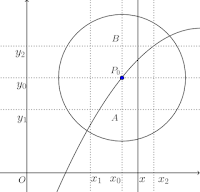
A(x₀,y₁)を近傍内の点とすると、y₁<y₀でf(x₀,y₁)<0、B(x₀,y₂)、y₀<y₂でf(x₂,y₂)>0である。

x₁≦x≦x₂において

f(x,y)は連続で単調増加だから、中間値の定理よりy₁<y<y₂となるyがただ１つ存在する。そのyの値はxの関数で、それをy=φ(x)とすればよい。

次に、y=φ(x)が連続であることを示す。α∈[x₁,x₂]、β=φ(α)とし、任意のε>0に対して

とすると、

y₁≦y≦y₂のとき、だから

はx=αで連続であるから、あるδ>0があって、

また、だから

よって、

となり、y=φ(x)はx=αで連続である。

f(x,y)はC¹級だから平均値の定理より

となるθが存在する。

また、f(x+Δx,y+Δy)=f(x,y)=0だから、Δx≠0のとき

は連続だから、Δx→0のとき、

（証明終）

３変数関数についても陰関数定理が成り立つ。

定理

関数f(x,y,z)が点(a,b,c)の近傍でC¹級ならば、点(a,b)を含む開集合D上でC¹級の関数z=φ(x,y)で

を満たすものがただ１つ存在し、

である。

問　次の問に答えよ。

（１）　点(1/√2,−1/√2)の近傍で、関係式x²+y²=1で定まる陰関数yを求めよ。

（２）　点(1,0)の近傍で、関係式x²+y²=1で定まる陰関数を求めよ。

【解】

（１）　f(x,y)=x²+y²–1=0とおくと。

よって、

となり、陰関数定理より、点(1/√2,−1/√2)の近傍で 関係式x²+y²=1で定まる陰関数y=φ(x)が存在する。

とすると、

となり不適。

とすると、

よって、

（２）　点(1,0)における偏微分係数は

だから、陰関数定理により点(1,0)の近傍で 関係式x²+y²=1で定まる陰関数x=φ(y)が存在する。

x²+y²=1をxについて解くと

(x,y)=(1,0)を満たすのはだから、これが点(1,0)の近傍で関係式x²+y²=1で定まる陰関数である。

（解答終）