２階常微分方程式の境界値問題を選点法で解く２

２階常微分方程式の境界値問題を選点法で解く２

問題　次の微分方程式を解け。

【答】

前回、この微分方程式の解を

と近似し、残差

をとし、重み関数wにディラックのデルタ関数

をとり、

となるようにを定める有限要素法の選点法を用い、選点を1/2とすることにより、

という近似解を得た。

しかし、こうして得た近似解の誤差が大きかったので、より精度のよい近似解を求める方法を考える。

そこで、（１）式を

とおくと、

となる。

このとき、

となるので、残差は

となる。

未知数がa₁、a₂の２つなので、これを定めるために選点をx=1/4とx=1/2に選び、その位置での残差を0とすると、

（１０）と（１１）から

という連立方程式が得られ、これを解くと、

となり、

という近似解が得られる。

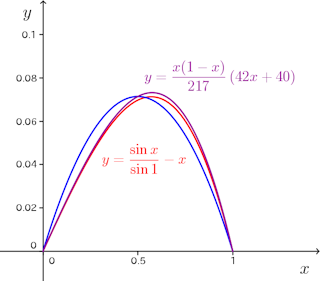
計算結果を右図に示す。

（１２）は（６）よりも厳密解（１）からの乖離が小さくなり、（１）の挙動をよく捉えていることが分かる。

（９）式の

とおくと、

と表すことができる。このψ₁、ψ₂を試行関数（Trial Function）と呼ぶ。

さらに、

とおくと、微分方程式は

と書くことができ、残差は

で表すことができる。

より一般的に、

これに重み関数をかけ、

となるように、この連立方程式（１５）から、未知数を定め、微分方程式（１３）の近似解を有限要素法の重み付き残差法という。

この重み関数のディラックのデルタ関数

を用いるものを選点法といい、デルタ関数の性質から

になる。

n=2のとき、未知数はa₁、a₂の２つだから、点をx₁、x₂の２点を選び、連立方程式

を解くことによって、a₁、a₂を定めることができる。

これが計算の仕組みというわけ。