第８回　開集合

前回、開集合について少しだけ話した。

開集合とは、

任意のa∈Aに対して、

　　

となるε>0が存在するが成り立つ集合のことだ。

そして、これは、
すべてのa∈AがAの内点、すなわち、aのε近傍である
ということと同じこと。

つまり、

 　　

ということ。

話は前後するが、Aの補集合の内点を外点といい、外点のすべての集まりを集合Aの外部といい、記号で表したりする。

で、この外点aと集合Aには次のような関係がある。
a∈Xに対して

　　

となるε>0が存在する。

さらに、全体の集合Xからを取り除いたもの、

　　

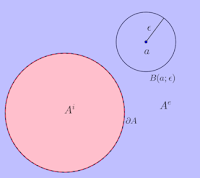
を境界といい、記号∂Aなどで表したりする。

抽象的でわかりづらいと思うのですが、例えば、

　　

という集合Aがあったとする。
これは原点Oを中心とする半径１の円とその内部のこと。
じゃ、Aの内部はというと、

　　

ただし、Aの外部は

　　

になる。

で、この境界∂Aは

　　

になるといういう当たり前の話。

そして、これらのことから、このことからわかるけれど、

　　言い忘れたんだけれど、

　　

という関係がある。Aの内部なんだから、Aに包まれるの当たり前の話だにゃ。特別難しいことをいっているわけじゃない。

なのだけれど、

理論的整合性を持たせるために、Aが空集合の時にも

　　

や

　　

とする。

さらに、集合の包含関係として、任意の集合Aに対して

　　

とする。

このあたりは定義なので、「何故？」なんて考えてはいけない。

こういうふうに定義する。