第１０回 正規分布２

第１０回　正規分布２

標準正規分布

平均m、分散σ²の正規分布をであらわす。

確率密度関数f(x)は

だから、

とおけば、

だから、確率変数zは

に従う。

これは、（１）のm=0、σ²=1とした形になっているから、平均0、分散1の正規分布である。これを標準正規分布という。

（２）で定義される変換を標準化変換という。

また、

である。

問１　確率変数Xが正規分布N(30,4²)に従うとき、

次の確率を求めよ。

【解】

とおくと、zはN(0,1)にしたがう。

（１）　x=30のときz=0、x=34のときz=1。

よって、

（２）　x=24のときz=−1.5、x=36のときz=1.5。

よって、

（３）　x=34のときz=1、x=38のときz=2。

よって、

（４）　x=24のとき、z=-1.5。

よって、

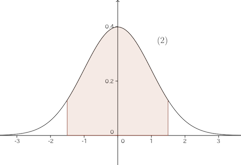
（註）　標準正規分布曲線はy軸に関して対称だからP(Z≦−1.5)=P(Z≧1.5)。したがって、

P(0≦Z≦1.5)はハッチングを施した部分。

（解答終了）

問２　ある高等学校３年生男子３００人の身長を測定したら、平均値165cm、標準偏差5cmで、正規分布に近い分布をしていた。

（１）　身長が１６０ｃｍ、１７０ｃｍ未満である生徒はおよそ何人か。

（２）　身長が１７３ｃｍ以上の生徒はおよそ何人か。

【解】

身長をXｃｍとすると、確率変数

は正規分布N(0,1)にしたがう。

（１）

正規分布表より

よって、求めるべき人数は

300×0.6826=204.78≒205（人）

（２）

だから、

ゆえに、求める人数は

300×0.0548=16.44≒16（人）

（解答終了）

問３　５００人の生徒にテスト（１００点満点）を行ったところ、その成績は、平均６５点、標準偏差１０点で、正規分布に近い分布をしていた。

（１）　成績が５５点以上、７５点以下の生徒はおよそ何人か。

（２）　成績が５０点以下の生徒はおよそ何人か。

（３）　上から１００番以内に入るためには、およそ何点以上とればいいか。

【解】

テストの得点をXとすると、

は正規分布N(0,1)にしたがう。

（１）

したがって、

500×0.6826=341.3≒341（人）

（２）

したがって、

500×0.1668=83.4≒83（人）

（３）　１００番は、全体の上から100÷500=0.2にあたる。

N(z)=0.5−0.2=0.3になるz≒0.84。

z=0.84に該当する得点をxとすると

したがって、７４点とればよい。

（解答終了）

ちなみに、５５点、７５点の偏差値は４０、６０。

５０点の偏差値は３５、７４の偏差値は５９です。