第１回 初等幾何の公理

第１回　初等幾何の公理

これからやる初等幾何の内容は、公理に基づく幾何学です。また、直線や円、さらに中点や中線といった中学で習う数学、幾何の用語を知っていることを前提として議論を展開します。

§０　用語の説明

公理と定理

すべての証明の出発点として、いくつかのそれ自身は証明せずに正しいものと認め、他のことがらを推論する基礎となるものを公理という。また、公理をもとにして正しいことが証明されたものを定理という。

定義と無定義用語

用語や記号などの意味を明確に定めた文章を定義という。点や直線などは定義しないで無定義用語として、そのまま用いる。

合同の定義

２つの図形があって、一方を移動したり、裏返したりして、ちょうど他方に重ね合わすことができるとき、この２つの図形は合同であるという。

平行線の定義

同一平面上にある２直線が共有点を持たないとき、この２直線は平行であるという。

§１　平面幾何の公理

平面幾何の公理には、次のようなものがある。

（１）　結合の公理　２点を通る直線はただ１つである

（２）　運動の公理　図形は、その形や大きさを変えないで、移動したり、裏返したりすることができる

（３）　平行線の公理　直言外の１点を通り、この直線に平行な直線はただ１つである

さらに、次の公理を加えたりするにゃ。

（４）　間と分割の公理

①　１直線上の異なる３点、A、B、Cについて、次のいずれかが成り立つ。

　（ア）　BがC、Aの間にある

　（イ）　BがACの間にない

②　１直線上にない異なる３点、A、B、Cと、これらの点を通らない直線lについて、次の関係のうちただ一つが成り立つ。

　（ア）　lは三角形ABCの２辺と交わる

　（イ）　lは三角形ABCのどの２辺とも交わらない

（４）の間と分割の公理のかわりに、次のパッシュの公理を採用するものもある。

パッシュの公理

平面上の１直線は、この平面を２つの側に分け、同じ側の２点を結ぶ線分上の点はすべて同じ側にあり、異なる側の２点を結ぶ線分はもとの直線と交わる

さらに、次のようなものなどを公理として採用し、出発点とする。

（１）　a=a

（２）　a=bならばb=a

（３）　a=b、b=cならば、a=c

（４）　a-b、c=dならば、a+c=b+d、a−c=b−d

§２　直線の角度と対頂角

直線の角度は、２直角、１８０°である、と定義する。

定理１

「対頂角α、βは等しい」

【証明】

α+γ=180°

β+γ=180°

よって、

α+γ=β+γ

∴α=β

§３　平行線と角

定理２

２つの直線に１つの直線が交わってできる１組の錯角が等しいとき、はじめの２直線は平行である。

【証明」

２直線にa、bに他の直線cが交わってできる錯角をα、βとし、aとbが平行でないと仮定する。

この図形をABの中点Oのまわりに回転し、点Aが点Bの位置に、点Bが点Aの位置にくるようにすると、ABとBAが重なる。

仮定より錯角α=βなので、直線a、直線bは重なる。

点Pの移った点をP’とすれば、点Pと点P'は相異なる２点となる。

異なる２点を通る直線が２本あることになり、結合の公理に反する。

よって、直線aと直線bは平行である。

定理３

平行な２直線が他の直線と交わってできる錯角は等しい。

【証明】
平行な２直線をa、bとし、この２直線に交わる直線をcとする。aとc、bとcが交わってできる錯角をそれぞれα、βとする。

α≠βと仮定する。

点Bを通り、cと角αになる直線b'をひく。

定理２より、aとb'は平行になり、点Bを通りaに平行な直線が２本存在することになり、不合理。

よって、α=βである。

この定理１、２、３から、次の定理が得られる。

定理４　２つの直線が１つの直線と交わってできる同位角は等しいならば、この直線は平行である。また、平行線に１つの直線が交わるとき、同位角は等しい。

中学校で習った「平行線の錯角（同位角）は等しい、錯角（同位角）が等しければ２直線は平行である」という平行線の性質が証明されたということになる。

§４　三角形と角

この定理３を使うと、三角形の内角の和が２直角、１８０°であることが次のように証明される。

定理５（三角形の内角定理）

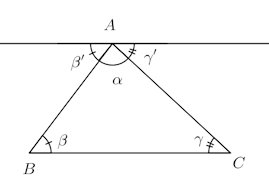
三角形の内角の和は２直角である。

【証明】

頂点Aを通り、BCに平行な直線をひく。

定理３よりβ=β'、α=α’。

また、α+β'+γ’=２直角=180°

よって、

α+β+γ=２直角=180°

（証明終わり）

さらに、定理４を用いると、次の三角形の外角定理が証明される。

定理６（三角形の外角定理）

【証明】

頂点CをとおりABに平行な直線をひく。

定理３よりα=α’、定理４よりβ＝β’

よって、

α+β=α’+β’

（証明終わり）

問題１

定理６を用いて定理５「三角形の内角の和は２直角である」を証明せよ。

例題１

下図のx°を求めよ。

【解】

直線lとmに平行な直線を次のように引けば、x=α+βになることが分かる。

だから、求める角度x°=45°+30°=75°

問題２　下の図で、lとmが平行である。∠xの大きさを求めよ。

【ヒント】　平行線を２本引け！！

問題３　下の図で、BP、CPはそれぞれ、∠ABC、∠ACBの二等分線である。∠A=64°のとき、∠BPCは何度か。

【答】　この図を書いたお絵描きソフトによると、１２２°。

問題４　次の定理を証明せよ。

定理　

「平行な２直線の一方と交わる直線は他方にも交わる」

【証明】

平行な２直線をa、bとし、直線cがaの交点をAとする。

cがbと交わらないと仮定する。

cとbは交わらないので、cとbは平行。

であるとすると、点Aを通るbに平行な直線が２本引けることになり、平行線の公理に反し、不合理。

よって、

「平行な２直線の一方と交わる直線は他方にも交わる」

（証明終わり）

問題５　次の定理を証明せよ。

定理

「異なる２直線が共有点をもつとき、共有点は１つである。」

【証明】

２直線a、bが２点A、Bを共有点をもつと仮定する。

結合の定理より、２点A、Bを通る直線は１つだけであり、a、bは同一の直線となって、「異なる２直線」に反し、不合理である。

よって、

「異なる２直線が共有点をもつとき、共有点は１つである。」

（証明終わり）